Gleitpfadoptimierung - wie kann ich am weitesten gleiten?
(von Klemens Ekschmitt)

Letztens bin ich nur ganz knapp am Landeplatz angekommen, obwohl die Strecke bei besserem Wetter gar kein Problem ist. Aber diesmal war der ganze Flug ein zähes Feilschen um jeden Meter Höhe. Beim Fliegen habe ich lauthals geflucht, zuhause habe ich mir dann die Flugstrategie für den besten Gleitpfad nochmal gründlich ausgeknobelt.

Als weitverbreitetes Beispiel habe ich die Polare vom Arcus nachgebaut (Abb. 1). Mein Nachbau ist ein bisschen langsamer geraten als das Original (34 statt 35 km/h Trimmgeschwindigkeit) und er hat auch eine etwas schlechtere maximale Gleitzahl (7,6 statt 7,8).

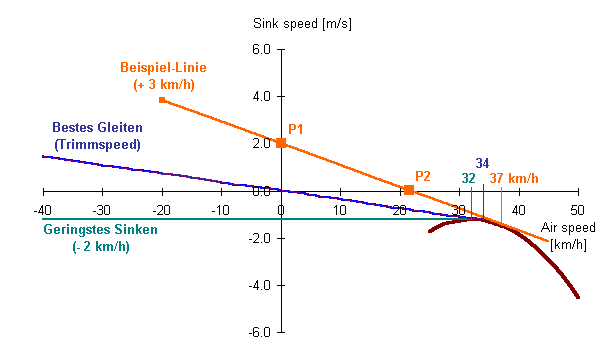
Die Achsen des Koordinatenkreuzes habe ich nach oben und links verlängert, aus folgendem Grund: Für die Bestimmung des besten Gleitwinkels gegenüber der Luft braucht man die Achsenverlängerung nicht. Dafür legt man durch den Nullpunkt (x=0; y=0) des Koordinatenkreuzes die Tangente an die Gleitschirm-Polare und erhält die Linie 'Bestes Gleiten'. Den besten Gleitpfad gegenüber Grund kann man aber bestimmen, indem man die Luftbewegung gegenüber Grund zur Schirmbewegung addiert, und hierfür kann man die Achsenverlängerung gebrauchen. Wenn ich zum Beispiel in einem Luftpaket fliege, daß 2m senkrecht nach unten sinkt (das Vario zeigt dann 2 m/s Luftmassensinken + 1,2 m/s Schirmsinken = 3,2 m/s), dann geht die passende Tangente nicht durch den Nullpunkt, sondern durch den Punkt (x=0; y=2,0) und entspricht der Linie '3 km/h beschleunigt'. Bei 2m Luftmassensinken müßte ich 3 km/h schneller fliegen als Trimmgeschwindigkeit, um den besten Gleitwinkel gegenüber Grund zu erfliegen. Die Graphik zeigt, daß 2 m/s Luftsinken nicht die einzige Situation ist, bei der diese Geschwindigkeit optimal ist. Zum Beispiel ergibt 22 km/h Gegenwind und 0 m/s Luftmassensinken die gleiche Linie. Jede Tangentenlinie bezeichnet jeweils alle diejenigen Kombinationen aus horizontaler Windkomponente (Gegenwind, Rückenwind) und vertikaler Windkomponente (Aufwind, Abwind), bei denen die zugehörige Schirmgeschwindigkeit den optimalen Gleitpfad gegenüber Grund bringt.

Abb. 1: Polare mit erweiterten Achsen

Damit ich nicht jedes Mal die Linie neu zeichnen muss, habe ich mir einen Satz von Tangenten ausgerechnet und in Abb. 2 eingetragen. Die neue Abbildung hat zwar einen gewissen ästhetischen Reiz und enthält auch die gewünschten Informationen, aber sie ist nicht so richtig übersichtlich. Ich habe deshalb Auszüge aus dieser Abbildung hergestellt, um vier Fragen zu beantworten:

1. Wann muss ich reagieren – unter welchen Bedingungen muß ich beschleunigen oder bremsen, um den besten Gleitpfad gegenüber Grund zu fliegen?
2. Wie stark muss ich reagieren – wie viel schneller oder langsamer als Trimmspeed bringt den besten Gleitpfad?
3. Wie exakt muss ich das Optimum einhalten– wieviel Gleitpfad verschenke ich, wenn ich gegenüber der optimalen Geschwindigkeit zu langsam oder zu schnell fliege?
4. Wieviel kann ich den Gleitpfad durch sauberes Fliegen überhaupt verbessern?

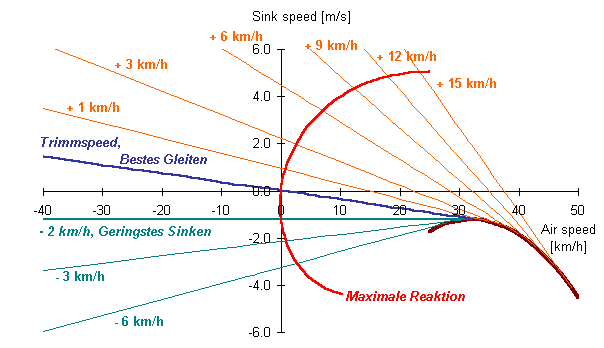Abb. 2: Polare mit Gleitlinien

Bleiben wir aber noch kurz bei Abb. 2, um ein paar Einzelheiten zu erklären. Die Tangenten habe ich jeweils nur bis zum Berührungspunkt mit der Polaren gezeichnet, und nicht nach rechts darüber hinaus. Rechts von der Polare ist der Gegenwind schneller als der Schirm, und der Schirm fliegt gegenüber Grund rückwärts. Rückwärtsfliegen habe ich auch in allen folgenden Darstellungen nicht berücksichtigt.

Die Abbildung enthält zusätzlich zur Polare (braun) noch zwei fett hervorgehobene Linien: Trimmspeed (blau) und Maximale Reaktion (rot). Die blaue Linie verbindet diejenigen Punkte, bei denen der Schirm von sich aus den besten Gleitpfad gegenüber Grund fliegt – hier ist keine Verbesserung des Gleitpfades möglich. Die rote Linie verbindet dagegen diejenigen Kombinationen aus horizontaler und vertikaler Windkomponente, bei denen eine Luftbewegung bestimmter Stärke eine maximale Korrektur der Geschwindigkeit erfordert. (Sie verbindet die Lotpunkte der Tangenten auf 0/0 und berücksichtigt dabei die unterschiedliche Skalierung der Achsen). Die blaue und die rote Linie spannen das Optimierungs-Feld auf zwischen "Geschwindigkeitsänderung bringt nichts" (blau) und "Geschwindigkeitsänderung bringt am meisten" (rot).

Ich habe überlegt und rumgerechnet, auf welche Weise ich die Gleitpfadoptimierung beim Fliegen am besten abschätzen kann. Mir sind zwei Methoden eingefallen, die sich darin unterscheiden, welchen Vergleichsstandpunkt man gedanklich einnimmt: Die erste setzt den Fixpunkt in den fliegenden Piloten und betrachtet die Wirkung der Windkomponenten auf den Flug. Die zweite setzt den Fixpunkt auf den Boden und betrachtet die Flugbahn gegenüber Grund.

Abschätzung der Gleitpfadoptimierung nach den Windkomponenten

Das Optimierungs-Feld aus Abb. 2 bildet eine Art "Wind-Tulpe" um den Piloten (Der Begriff "Windrose" ist leider schon vergeben). Stellt man den Wind als Vektor dar, der auf den Piloten gerichtet ist, dann zeigt Abb. 3, welche Windrichtungen eine Anpassung der Schirm-Geschwindigkeit am dringendsten erfordern. In der Abbildung fliegt der Pilot an einem flachen Hang. Der Wind weht kräftig hangaufwärts parallel zur Hangneigung und greift flach unter den Gleitwinkel. Er hebt den Gleitpfad an, und der Pilot könnte anbremsen (grüne Zone). Bergwind an dem gleichen Hang würde von links oben auf den Gleitwinkel drücken, und der Pilot sollte beschleunigen (rote Zone). Allerdings verläuft der Windpfeil in beiden Fällen nahe an der blauen Linie. Der Pfeilschaft liegt weit von der rot-grünen Kurve entfernt und eine Geschwindigkeits­Anpassung ist nicht sehr dringend und auch nicht sehr wirksam.

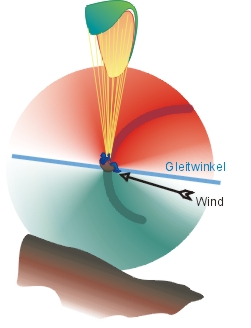Abb. 3: Die "Wind-Tulpe" für die Gleitpfadoptimierung

Aus Abb. 3 ergeben sich drei Faustregeln:

1. Winde parallel zum Gleitwinkel erfordern keine Geschwindigkeitsanpassung (es sei denn, man wird bei starkem Gegenwind rückwärts gepustet).
2. Bei schwachen Luftbewegungen (< 5km/h) verläuft die rot-grüne Kurve fast senkrecht, und man sollte vor allem auf vertikale Windkomponenten reagieren. Dann lässt sich gut nach dem Vario fliegen.
3. Bei stärkeren Luftbewegungen gewinnt die horizontale Windkomponente an Bedeutung, vor allem bei Gegenwind. Dann muß man horizontale und vertikale Windkomponenten berücksichtigen. Entweder indem man mit voller Instrumentierung fliegt, oder indem man die Windkomponenten z.B. nach der Hangneigung schätzt.

Die Wind-Tulpe in Abb. 3 zeigt, wann Beschleunigen bzw. Anbremsen am meisten bringt, aber nicht, wie viel davon jeweils optimal ist. Dafür muß man sich wieder die Gleitlinien in Abb. 2 anschauen. Da ich mir unter den abstrakten Windkomponenten in der Abbildung (x km/h Gegenwind, y m/s Aufwind) nicht immer gleich was vorstellen kann, habe ich typische Windsituationen in die Gleitlinien-Graphik eingetragen. Zum Beispiel bedeutet Talwind normalerweise, daß ich am Hang gleichzeitig Gegenwind und Aufwind habe. Anschließend habe ich noch ein paar überflüssige Gleitlinien aus der Abbildung entfernt. Das Ergebnis hat mich dann doch überrascht (Abb. 4).

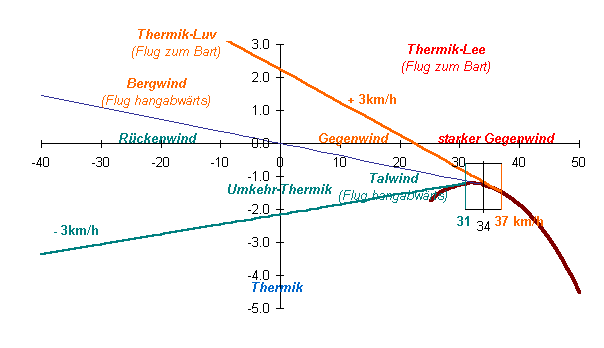Abb. 4: Polare und "Windkarte" mit typischen Windsituationen

Mit dem mickrigen Geschwindigkeitsfenster von 31 - 37 km/h decke ich für fast alle Windsituationen die optimalen Gleitpfade gegenüber Grund ab. Das gilt für die gut fliegbaren Situationen, wie Gegenwind, Bergwind, Talwind und Umkehrthermik , und dazu auch noch für heftigere Flugsituationen, wie starken Rückenwind und den Einstieg aus Luv in den Bart. Da braucht es schon sensible Händchen und Füßchen, um innerhalb dieses Fensterchens den optimalen speed zu bremsen oder zu treten. Vielleicht doch lieber Ballettsocken statt Stiefel?

Beschleunigen um mehr als 3 km/h verbessert den Gleitwinkel nur bei starkem Gegenwind (> 20 km/h) oder bei Gegenwind mit Abwind, z.B. im Lee eines Barts.

In der Thermik ist natürlich Thermik-Fliegen angesagt und nicht Gleiten.

Abschätzung der Gleitpfadoptimierung aus dem Gleitpfad selbst

Außer durch die Windkomponenten kann die Gleitpfadoptimierung auch aus dem Gleitpfad gegenüber Grund abgeschätzt werden. Hierfür habe ich die Gleitlinien-Grafik so umgerechnet, dass anstatt der horizontalen und vertikalen Windkomponente, die horizontale und vertikale Geschwindigkeit des Schirms gegenüber Grund auf den Koordinatenachsen aufgetragen sind. Die Achsen sind maßstabsgetreu skaliert, so daß die Neigung der Linien dem Gleitpfad im Gelände entspricht. Die Grafik macht deutlich, dass jeweils eine bestimmte Schirmgeschwindigkeit und ein bestimmter Gleitpfad optimal zusammengehören. Man sollte beim Fliegen die Geschwindigkeit (und damit zusätzlich auch den Gleitpfad) so regulieren, dass Schirmgeschwindigkeit und Gleitpfad entsprechend der Abbildung zusammenfallen. Ist der Gleitpfad zu steil, sollte man schneller fliegen. Ist der Gleitpfad flacher, sollte man langsamer fliegen. Die Abschätzung nach dem Gleitpfad hat den Vorteil, dass man sich für seinen Schirm eine Tabelle machen kann, in der optimale Kombinationen von Gleitwinkel und Schirmgeschwindigkeit aufgelistet sind (Tab. 1). Rechnerisch günstiger ist es, wenn man anstelle des Gleitpfads (= x/y) den "Steigpfad" nimmt, also den Kehrwert davon (= y/x). Die Beziehung zwischen Steigpfad und optimaler Schirmgeschwindigkeit ist fast linear. (Der Steigpfad ist identisch mit der Steigung der Polare bei der entsprechenden Schirmgeschwindigkeit).

Die Abschätzung der Gleitpfadoptimierung nach dem Gleitpfad hat den Nachteil, dass sie die Windsituation im Gelände nicht so deutlich widerspiegelt wie die erste Methode. In der Bewegung gegenüber Grund überlagern sich Windgeschwindigkeit und Schirmgeschwindigkeit. Die Wind-Tulpe (rote + blaue Linie) ist durch diese Überlagerung stark verzerrt und läßt sich nicht gut interpretieren.

Tab. 1: Gleitpfadoptimierung für das verwendete Profil (stark gerundete Werte)

Wieviel Gleitpfad verliere ich durch ungenaues Fliegen?

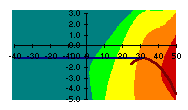
Das Geschwindigkeitsfenster für optimales Gleiten ist unter normalen Flugbedingungen so eng, dass ich auf jeden Fall damit rechnen muss, dass ich die ideale Geschwindigkeit nicht genau einhalte. In der nächsten Abbildung (Abb. 6) habe ich mir deshalb eingezeichnet, wie viel Prozent der Gleitstrecke ich verliere, wenn ich 1, 2 oder 3 km/h langsamer, bzw. 1, 2 oder 3 km/h schneller fliege, als optimal wäre. Bei Situationen, in denen der Schirm steigt, habe ich Verluste des Steigens statt Verlusten der Gleitstrecke eingezeichnet. Für die Grenze zwischen Steigen und Sinken ist die Gleitzahl mathematisch nicht definiert (der Flug ist waagerecht und die Gleitzahl ist unendlich groß). Ich habe diese Linie in der Berechnung ausgespart. Theoretisch bringt hier jede Abweichung vom Optimum extrem große Verluste, weil statt des waagerechten Flugs ein sinkender Flug entsteht.

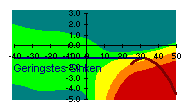
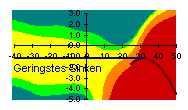
Die dunkelgrünen Flächen bezeichnen geringe Verluste bis 3%. Hellgrün ist auch noch erträglich: bis 10% der optimalen Gleitstrecke. Gelbe Flächen bezeichnen schon bis zu 30% Verlust, und bei orange (bis 60%) und rot (bis 100%) wird es dann mulmig. Die einzelnen Beulen und Wellen in den Farbflächen muß man nicht zu ernst nehmen, weil sie von dem graphischen Interpolationsverfahren herrühren, das ich benutzt habe. Die zwei kritischen Zonen lassen sich aber gut erkennen: Es sind die Situationen in denen der Schirm in horizontaler oder vertikaler Richtung gerade zum Stillstand gebracht wird, also starker Gegenwind und schwacher Aufwind.

Zuviel gebremst
1 km/h zu langsam	2 km/h zu langsam	3 km/h zu langsam
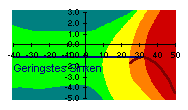
Zuviel beschleunigt
1 km/h zu schnell	2 km/h zu schnell	3 km/h zu schnell
Verluste in % des Optimums   0 - 3%   3 - 10%   10-30%   30-60%   > 60%
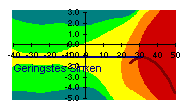
Abb. 6: Gleitpfadverluste bei zu langsamem und zu schnellem Fliegen

Der kritischste Situation ist bei Gegenwind mit Stärken in der Nähe der Schirmgeschwindigkeit, deutlich markiert durch die orangen und roten senkrecht orientierten Flächen. Hier verschlechtert jeder km/h zu viel oder zu wenig den Gleitpfad erheblich. Bei Rückenwind ist die Sache viel entspannter – alles schön grün.

Die zweite kritische Situation ist bei schwachem Aufwind, der gerade das Schirmsinken kompensiert. Schon ab 1 km/h Abweichung vom Optimum entstehen hellgrüne und gelbe Streifen entlang der Linie "Geringstes Sinken". Hier wirkt sich unsauberes Fliegen ebenfalls negativ aus, auch bei Rückenwind.

Wieviel Gleitpfad kann ich denn rausholen?

Zum Schluß das Wichtigste: Wofür lohnt sich der ganze Aufwand? Die letzte Abbildung zeigt, wie viel Prozent Gleitpfad (bzw. wie viel Prozent Steigen) ich gewinnen kann, wenn ich den Gleitpfad optimiere, anstatt einfach Trimmspeed zu fliegen.

Die Lage der Flächen in der Abbildung ist sehr ungenau. Z.B. sollte der Bereich entlang der blauen Linie (Bestes Gleiten; Trimmspeed) natürlich weiss sein, weil hier der Gleitpfad nicht mehr verbessert werden kann. Da kriegt die graphische Interpolation die Kurve nicht. Die Abbildung zeigt aber die grobe Lage und vor allem die Größenordnung der erzielbaren Verbesserungen richtig:

Bei Rückenwind mit Abwind (=Bergwind) ist nicht viel zu holen. Nur bei sehr starken Abwinden kann man den Gleitwinkel etwas verbessern. Bei Rückenwind und Aufwind (z.B. in der Umkehr-Thermik) sind dagegen 3-10% Gleitpfad-Gewinn drin. Die Gleitpfadoptimierung lohnt sich vor allem bei Gegenwind. Bei mittlerem Gegenwind kann der Gleitpfad bis zu 30% verbessert werden, und bei zunehmendem Gegenwind entsprechend mehr. Es lohnt sich also.

Allerdings gelten diese Zahlen für die hier verwendete Polare eines Basis-Intermediates. Bei Schirmen mit einer flacheren Polare verändert sich der Gleitpfad weniger, wenn beschleunigt oder gebremst wird. Dementsprechend weniger muß man sich dann um den Gleitpfad Gedanken machen. Fliegen mit optimalem Gleitpfad ist ja auch nicht alles - meistens wollen wir lieber schneller fliegen, sicherer fliegen, oder sonstwie rumdüsen. Außerdem bringt die geschickte Wahl der Flugroute mit ein, zwei Hebern mehr, als die perfekte Gleitfahrt an diesen Hebern vorbei. Trotzdem ist es vielleicht gut zu wissen, wie man in der Not einige Höhenmeter sparen kann. Ich werd's versuchen ...

Korrekturen, Kommentare und Ergänzungen sind jederzeit willkommen Klemens